Podemos empezar afirmando que una empresa producirá siempre que le compense hacerlo. Y le compensará o no dependiendo de la relación entre lo que le cuesta producir –y vender– y lo que cobra por el producto. Si lo que cobra es más de lo que le cuesta, producirá; si no, debería parar la producción para, así, perder menos. Por ejemplo, imaginemos que somos los gestores de una fábrica de relojes. Si producir y vender un reloj nos cuesta 100 u.m. (unidades monetarias) de media y lo podemos vender a 130 u.m., estamos ganando un 30% en cada reloj; mientras que si sólo lo podemos vender a 80 u.m. no deberíamos producir ningún reloj ya que cada reloj producido y vendido hace que perdamos un 20%. Matizaremos esta afirmación más adelante.
Centrémonos ahora en el coste de esos relojes. En esas 100 u.m. están incluidas la materia prima necesaria para el reloj, las horas de mano de obra que pagamos a nuestros operarios, el consumo de electricidad, etc. Es decir, ahí incluimos varias categorías de coste que son función de la producción, a lo mejor no inmediatamente pero desde luego sí en el corto plazo. Estos gastos que pueden ser ajustados en el corto plazo al nivel de producción se denominan costes variables.
Hay otro tipo de gastos en una empresa que sólo pueden ser ajustados en el largo plazo. Nuestra empresa puede tener un taller donde fabricamos los relojes. Dado el tamaño de dicho taller y la maquinaria de que disponemos, nuestra capacidad de producción es de 100 relojes a la semana. Si quisiéramos incrementar esa capacidad de producción tendríamos que comprar nueva maquinaria y construir un nuevo taller o ampliar el actual. También podríamos alquilar un local y así estaríamos transformando en variable un coste que no lo es, lo cual –dependiendo de los precios de alquiler y de compra– puede ser rentable, pero ya tendría menos sentido alquilar también la maquinaria –supongamos que aún no se ha inventado el arrendamiento financiero–. Estos gastos que sólo pueden ser modificados en el largo plazo se conocen como costes fijos y su cuantía no depende del nivel de producción o, dicho de otra manera, si incrementamos –dentro de nuestras posibilidades– el nivel de producción, a corto plazo sólo varían los costes variables.
En las 100 u.m. que nos cuesta producir un reloj están incluidos tanto los costes variables como la parte proporcional de los costes fijos de la empresa. Es decir, el coste total es la suma de los costes fijos y de los costes variables.
Con los ingredientes que tenemos hasta ahora podemos hablar del concepto de punto muerto o umbral de rentabilidad, que es el nivel de producción a partir del que el resultado de la empresa –que era negativo– se hace nulo –y pasa a ser positivo. Pero este concepto no nos ayuda a saber si produciendo más –o menos– mejoramos nuestro resultado. Simplemente nos indica el momento a partir del cual la empresa pasa de dar pérdidas a dar beneficios.
Necesitamos pues introducir algún nuevo indicador que nos ayude a decidir si la empresa debe aumentar la producción, disminuirla o dejarla como está. Podemos definir el coste marginal como lo que se incrementa el coste total de la producción al incrementar en una unidad la misma. En realidad, el incremento de la producción debe ser infinitesimal en cuyo caso el coste marginal se define como la derivada del coste total, pero con quedarnos con la anterior idea es suficiente.
De igual forma, definiremos el ingreso marginal como la variación en nuestros ingresos por vender una unidad adicional. Para una empresa en competencia perfecta es evidente que el ingreso marginal es el precio de mercado de esa unidad adicional.
Pues bien, con todo eso encima de la mesa, podemos decir que una empresa producirá más si esa producción adicional es positiva para su resultado, es decir, si esa unidad adicional hace que sus pérdidas sean menores o que su beneficio sea mayor. Y seguirá produciendo más en tanto dicha condición se cumpla. Por otra parte, la empresa debe reducir su producción mientras haciéndolo mejore su beneficio o reduzca sus pérdidas, hasta que esa circunstancia deje de darse. En la práctica, y usando los conceptos que acabamos de introducir, una empresa producirá más si lo que ingresa por esa producción adicional –el precio– es mayor que lo que le cuesta esa producción adicional –el coste marginal–.
En realidad, las cosas no son tan fáciles ya que puede que estemos maximizando nuestro resultado –que al final es lo que logramos con el proceso descrito en el párrafo anterior– pero que aún así no estemos cubriendo nuestros costes ya que del hecho de que el coste marginal sea igual o superior al precio no podemos derivar que nuestro ingreso total sea capaz de cubrir todos nuestros costes. Pero esto es algo que trataremos en la siguiente entrada de esta serie.
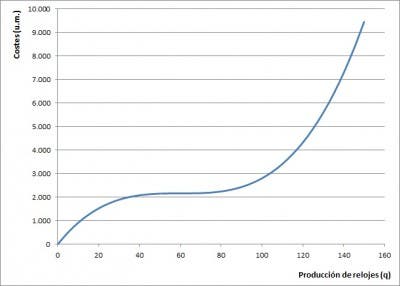
Veamos todo esto aplicado a nuestra fábrica de relojes. Supongamos que nuestros costes fijos son de 3.000 u.m. y que nuestros costes variables vienen dados por una función cuya gráfica es la que vemos a la izquierda.
En vez de una función de costes variables lineal, utilizamos una función de costes variables con esa forma para dar generalidad al razonamiento –y para que el coste marginal no sea constante–. En cualquier caso, esa forma tampoco es tan inusual cuando hablamos de costes. Al contrario. Es normal que en las primeras unidades de producción el ahorro de costes sea menor que en las unidades que están más próximas a la capacidad óptima de la empresa –tendremos recursos ociosos: máquinas, operarios, etc.–. Y también es normal que asumamos que llega un nivel de producción –quizás un poco por encima de la capacidad óptima de la empresa– que hace que los costes se disparen –requeriremos horas extras de nuestros operarios, las máquinas precisarán un mayor mantenimiento, etc.–.
| q | CF | CV | CT | CM | Ingreso | Resultado |
|---|---|---|---|---|---|---|
| 0 | 3.000 | 0 | 3.000 | 108 | 0 | -3.000 |
| 5 | 3.000 | 496 | 3.496 | 91 | 650 | -2.846 |
| 10 | 3.000 | 910 | 3.910 | 75 | 1.300 | -2.610 |
| 15 | 3.000 | 1.249 | 4.249 | 61 | 1.950 | -2.299 |
| 20 | 3.000 | 1.520 | 4.520 | 48 | 2.600 | -1.920 |
| 25 | 3.000 | 1.731 | 4.731 | 37 | 3.250 | -1.481 |
| 30 | 3.000 | 1.890 | 4.890 | 27 | 3.900 | -990 |
| 35 | 3.000 | 2.004 | 5.004 | 19 | 4.550 | -454 |
| 40 | 3.000 | 2.080 | 5.080 | 12 | 5.200 | 120 |
| 45 | 3.000 | 2.126 | 5.126 | 7 | 5.850 | 724 |
| 50 | 3.000 | 2.150 | 5.150 | 3 | 6.500 | 1.350 |
| 55 | 3.000 | 2.159 | 5.159 | 1 | 7.150 | 1.991 |
| 60 | 3.000 | 2.160 | 5.160 | 0 | 7.800 | 2.640 |
| 65 | 3.000 | 2.161 | 5.161 | 1 | 8.450 | 3.289 |
| 70 | 3.000 | 2.170 | 5.170 | 3 | 9.100 | 3.930 |
| 75 | 3.000 | 2.194 | 5.194 | 7 | 9.750 | 4.556 |
| 80 | 3.000 | 2.240 | 5.240 | 12 | 10.400 | 5.160 |
| 85 | 3.000 | 2.316 | 5.316 | 19 | 11.050 | 5.734 |
| 90 | 3.000 | 2.430 | 5.430 | 27 | 11.700 | 6.270 |
| 95 | 3.000 | 2.589 | 5.589 | 37 | 12.350 | 6.761 |
| 100 | 3.000 | 2.800 | 5.800 | 48 | 13.000 | 7.200 |
| 105 | 3.000 | 3.071 | 6.071 | 61 | 13.650 | 7.579 |
| 110 | 3.000 | 3.410 | 6.410 | 75 | 14.300 | 7.890 |
| 115 | 3.000 | 3.824 | 6.824 | 91 | 14.950 | 8.126 |
| 120 | 3.000 | 4.320 | 7.320 | 108 | 15.600 | 8.280 |
| 125 | 3.000 | 4.906 | 7.906 | 127 | 16.250 | 8.344 |
| 130 | 3.000 | 5.590 | 8.590 | 147 | 16.900 | 8.310 |
| 135 | 3.000 | 6.379 | 9.379 | 169 | 17.550 | 8.171 |
| 140 | 3.000 | 7.280 | 10.280 | 192 | 18.200 | 7.920 |
| 145 | 3.000 | 8.301 | 11.301 | 217 | 18.850 | 7.549 |
| 150 | 3.000 | 9.450 | 12.450 | 243 | 19.500 | 7.050 |
En la tabla anterior podemos ver los valores de costes fijos (CF), variables (CV) y totales (CT) según la producción de relojes (q). También incluimos una columna de coste marginal (CM): lo que varía el coste total –o únicamente el variable– de nuestra producción por incrementarla en una unidad –calculado como el valor de la derivada de la función de costes totales en cada nivel de producción–. Además, en las dos últimas columnas presentamos el ingreso total de la venta de la producción a un precio de 130 u.m. y el resultado calculado como la diferencia entre el ingreso total y el coste total para cada nivel de producción.
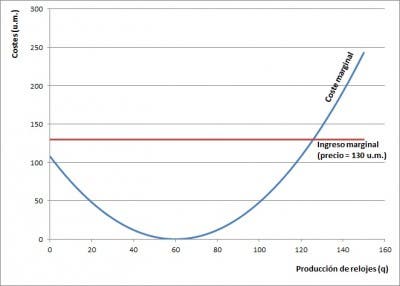
En la tabla también vemos cómo el coste marginal se iguala al precio de venta en algún sitio entre una producción de 125 y 130 relojes. En la gráfica de la derecha representamos el coste marginal de nuestra fábrica y el precio de venta de los relojes.
Nos faltaría por ver conjuntamente los costes totales, los ingresos totales y el resultado y comprobar que, en efecto, el máximo resultado se produce para la producción correspondiente al punto de corte entre la curva de coste marginal y el precio –la “curva” de ingreso marginal–. Pero, si decimos todo en la primera entrada, esto dejaría de ser una serie ¿no os parece? Así que dejamos en el aire algunas gráficas para tener algo que enseñar en la segunda entrada acerca de la Teoría de la Oferta.