En la anterior entrada de esta serie vimos cómo a una empresa le interesa producir más en tanto en cuanto lo que ingrese por esa producción adicional –el precio si la empresa opera en un mercado competitivo– iguale o supere lo que le cuesta esa producción adicional –el coste marginal–. Con este proceder, estamos maximizando el resultado. Pero también dijimos que puede que estemos maximizando nuestro resultado pero que aún así no estemos cubriendo nuestros costes por lo que tenemos que buscar una manera de asegurarnos esa circunstancia.
Introduciremos hoy el concepto de coste medio que no es otra cosa que lo que cuesta de media cada unidad de producción. Su cálculo es directo: es el resultado del cociente entre los costes totales y las unidades producidas. Esto si hablamos del coste total medio, puesto que también podemos calcular el coste fijo medio como cociente entre los costes fijos y las unidades producidas y el coste variable medio como cociente entre los costes variables y las unidades producidas.
Intuitivamente podemos darnos cuenta de que los costes fijos medios descenderán a medida que incrementamos el nivel de producción puesto que estamos dividiendo una cantidad fija entre un número cada vez mayor. En cambio, para decir algo acerca del comportamiento de los costes variables medios y de los costes totales medios tenemos que investigar un poco más. En principio, lo único que es seguro es que los costes totales medios siempre son superiores a los costes variables medios –puesto que los primeros también incluyen los costes fijos medios, por pequeños que sean–.
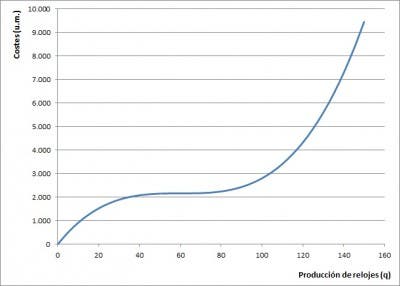
La función de costes variables que vimos en la anterior entrada y que reproducimos a la izquierda puede ser dividida en dos partes. La primera –hasta una producción de aproximadamente 60 unidades– en la que el coste variable crece cada vez menos a medida que incrementamos el nivel de producción; y la segunda –de 60 unidades en adelante– en la que el coste variable crece más que proporcionalmente con respecto al nivel de producción. Pensando en términos de costes medios, parece que ese comportamiento se traducirá en un coste medio decreciente hasta un determinado nivel de producción –superior a 60 unidades– y creciente a partir del mismo. No entraremos a deducir matemáticamente cuál es ese punto de mínimo coste medios; simplemente fijémonos en la siguiente tabla, donde recogemos los valores de costes (CF, CV y CT), costes medios –variables (CVMe) y totales (CTMe)– y coste marginal (CM) correspondientes a cada nivel de producción, y veamos como el coste variable medio decrece hasta una producción de 85-95 unidades y crece a partir de dicha producción. El coste total medio, por su parte, también decrece pero el nivel de producción en el que alcanza un mínimos es de 100-110 unidades.
| q | CF | CV | CT | CVMe | CTMe | CM |
|---|---|---|---|---|---|---|
| 0 | 3.000 | 0 | 3.000 | 0 | 0 | 108 |
| 5 | 3.000 | 496 | 3.496 | 99 | 699 | 91 |
| 10 | 3.000 | 910 | 3.910 | 91 | 391 | 75 |
| 15 | 3.000 | 1.249 | 4.249 | 83 | 283 | 61 |
| 20 | 3.000 | 1.520 | 4.520 | 76 | 226 | 48 |
| 25 | 3.000 | 1.731 | 4.731 | 69 | 189 | 37 |
| 30 | 3.000 | 1.890 | 4.890 | 63 | 163 | 27 |
| 35 | 3.000 | 2.004 | 5.004 | 57 | 143 | 19 |
| 40 | 3.000 | 2.080 | 5.080 | 52 | 127 | 12 |
| 45 | 3.000 | 2.126 | 5.126 | 47 | 114 | 7 |
| 50 | 3.000 | 2.150 | 5.150 | 43 | 103 | 3 |
| 55 | 3.000 | 2.159 | 5.159 | 39 | 94 | 1 |
| 60 | 3.000 | 2.160 | 5.160 | 36 | 86 | 0 |
| 65 | 3.000 | 2.161 | 5.161 | 33 | 79 | 1 |
| 70 | 3.000 | 2.170 | 5.170 | 31 | 74 | 3 |
| 75 | 3.000 | 2.194 | 5.194 | 29 | 69 | 7 |
| 80 | 3.000 | 2.240 | 5.240 | 28 | 66 | 12 |
| 85 | 3.000 | 2.316 | 5.316 | 27 | 63 | 19 |
| 90 | 3.000 | 2.430 | 5.430 | 27 | 60 | 27 |
| 95 | 3.000 | 2.589 | 5.589 | 27 | 59 | 37 |
| 100 | 3.000 | 2.800 | 5.800 | 28 | 58 | 48 |
| 105 | 3.000 | 3.071 | 6.071 | 29 | 58 | 61 |
| 110 | 3.000 | 3.410 | 6.410 | 31 | 58 | 75 |
| 115 | 3.000 | 3.824 | 6.824 | 33 | 59 | 91 |
| 120 | 3.000 | 4.320 | 7.320 | 36 | 61 | 108 |
| 125 | 3.000 | 4.906 | 7.906 | 39 | 63 | 127 |
| 130 | 3.000 | 5.590 | 8.590 | 43 | 66 | 147 |
| 135 | 3.000 | 6.379 | 9.379 | 47 | 69 | 169 |
| 140 | 3.000 | 7.280 | 10.280 | 52 | 73 | 192 |
| 145 | 3.000 | 8.301 | 11.301 | 57 | 78 | 217 |
| 150 | 3.000 | 9.450 | 12.450 | 63 | 83 | 243 |
Vemos en la gráfica de abajo cómo los mínimos de los costes medios, variables y totales, se producen justo en el punto de corte con la curva de coste marginal. Tampoco vamos a ver la justificación matemática de esta característica –su dificultad, así como la de la deducción de los mínimos de las curvas de coste medios, no es excesiva si tenéis interés y, en cualquier caso, no son pocos los libros o, si preferís, las páginas de Internet, donde podemos encontrar el aparato matemático que subyace tras esta teoría–.
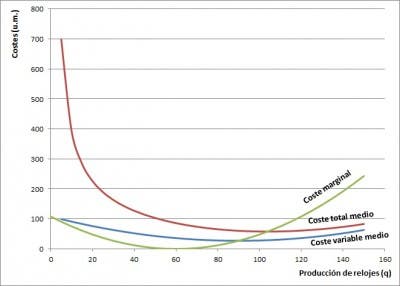
Pero, más allá de una mera casualidad, esa circunstancia es muy importante para saber cuál es la curva de oferta de una empresa en competencia. Dicha curva de oferta es la curva de coste marginal –hay que recordar lo que vimos en la anterior entrada– a partir del momento en que dicha curva corta a la de costes variables medios, pasando por el mínimo de ésta.
Antes de dicho punto de corte, antes –por tanto– del comienzo de la curva de oferta de la empresa, la curva de coste marginal está por debajo de la de coste variable medio, indicando que para los niveles de producción correspondientes a la empresa le compensa no producir en el corto plazo puesto que así por lo menos se ahorra el coste variable. En este caso, el resultado sería negativo por la cuantía de los costes fijos, que sólo pueden ser evitados si se decide cerrar definitivamente la empresa.
En otras palabras, nuestra fábrica de relojes no debería producir nunca menos de 85-95 relojes –siempre suponemos que es capaz de vender toda su producción para no complicar innecesariamente el modelo– puesto que en ese caso perdería más dinero que parando la producción. A partir de ese nivel de producción, la empresa comenzaría a recuperar los costes fijos hasta el momento en que la curva de oferta, la curva de coste marginal, corta a la curva de costes totales medios en su mínimo.
En nuestro ejemplo, el mínimo coste total medio tiene lugar para un nivel de producción de 100-105 relojes. A partir de ese punto, nuestra empresa comienza a dar resultados positivos. Antes del mismo –para niveles de producción por encima de 85-95 relojes–, a la empresa le compensa producir, aunque presente pérdidas, porque está recuperando todos los costes variables y parte de los costes fijos –y si no produjera perdería todos los costes fijos–.
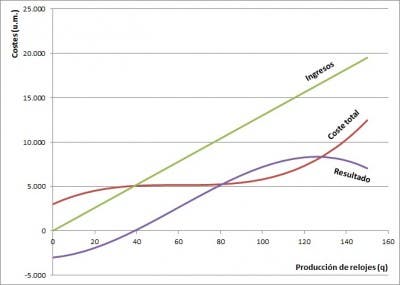
Todo lo visto puede ser expresado en función del precio de mercado de los relojes. Recordemos que la teoría económica nos dice que la oferta es función del precio –a pesar de que, por circunstancias históricas, el precio se representa en el eje vertical y la cantidad en el horizontal–. Así, nuestra empresa estaría dispuesta a producir 85-95 relojes si el precio de mercado de los mismos estuviese en 19-37 u.m. Si, en cambio, el precio de mercado sube a 48-61 u.m., nuestra fábrica produciría 100-105 relojes. Y para el precio de mercado con el que hemos estado trabajando en estas dos entradas, 130 u.m., la empresa producirá 125-130 relojes.
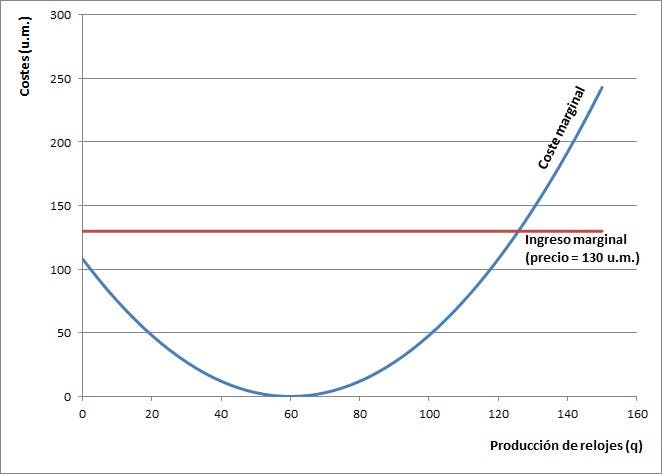
En la anterior gráfica representamos los ingresos correspondientes a un precio de 130 u.m. para cada nivel de producción, los costes totales en los que incurrimos y el resultado que obtenemos. Vemos cómo el nivel de producción que maximiza el resultado coincide con el punto de corte de las curvas de coste marginal e ingreso marginal que veíamos en la anterior entrada y que reproducimos de nuevo a la derecha.
Con esto terminamos de analizar cómo se comportan las empresas cuando operan en un mercado en competencia perfecta. Dejamos para futuras entradas el ver qué hacen cuando el mercado en el que operan es un oligopolio o un monopolio. ¿Y en qué afecta el tipo de mercado a la teoría de la oferta? En un mercado en competencia, la empresa no puede influir de ninguna manera ni sobre el precio ni sobre la cantidad de equilibrio del mercado; así, en lo que llevamos visto hasta ahora, siempre hemos considerado el precio como un dato, como algo que a la empresa le viene dado. Pero en los monopolios y oligopolios, la empresa puede hacer que suba el precio si decide disminuir la cantidad producida. Y viceversa: puede incrementar la cantidad producida para hacer que baje el precio –y así, por ejemplo, impedir la entrada de nuevos competidores–. Pero, como decimos, dejamos este desarrollo para la próxima entrada.